3d drawing of a person's face pushing through a wall

In technical drawing and computer graphics, a multiview projection is a technique of illustration by which a standardized series of orthographic ii-dimensional pictures are constructed to represent the form of a 3-dimensional object. Up to six pictures of an object are produced (chosen primary views), with each projection plane parallel to one of the coordinate axes of the object. The views are positioned relative to each other according to either of two schemes: outset-angle or 3rd-bending projection. In each, the appearances of views may exist thought of every bit being projected onto planes that form a six-sided box around the object. Although vi different sides can be fatigued, usually iii views of a drawing requite enough information to make a iii-dimensional object. These views are known as forepart view, top view and cease view. Other names for these views include plan, pinnacle and department. When the plane or axis of the object depicted is not parallel to the projection airplane, and where multiple sides of an object are visible in the same epitome, information technology is called an auxiliary view.

Overview [edit]

To render each such picture, a ray of sight (also called a project line, projection ray or line of sight) towards the object is chosen, which determines on the object various points of interest (for instance, the points that are visible when looking at the object along the ray of sight); those points of interest are mapped by an orthographic projection to points on some geometric airplane (called a projection airplane or paradigm aeroplane) that is perpendicular to the ray of sight, thereby creating a 2D representation of the 3D object.

Customarily, 2 rays of sight are chosen for each of the three axes of the object'south coordinate system; that is, parallel to each centrality, the object may be viewed in one of 2 opposite directions, making for a full of vi orthographic projections (or "views") of the object:^[1]

• Along a vertical axis (frequently the y-axis): The top and lesser views, which are known equally plans (because they show the arrangement of features on a horizontal plane, such as a floor in a building).
• Forth a horizontal axis (often the z-axis): The front and dorsum views, which are known as elevations (considering they show the heights of features of an object such as a building).
• Along an orthogonal axis (often the x-axis): The left and right views, which are too known as elevations, following the same reasoning.

These six planes of projection intersect each other, forming a box effectually the object, the most uniform construction of which is a cube; traditionally, these half-dozen views are presented together past first projecting the 3D object onto the 2D faces of a cube, then "unfolding" the faces of the cube such that all of them are contained within the aforementioned aeroplane (namely, the aeroplane of the medium on which all of the images volition be presented together, such equally a piece of paper, or a computer monitor, etc.). However, fifty-fifty if the faces of the box are unfolded in one standardized style, in that location is ambiguity as to which projection is being displayed by a particular confront; the cube has two faces that are perpendicular to a ray of sight, and the points of interest may be projected onto either one of them, a choice which has resulted in 2 predominant standards of projection:

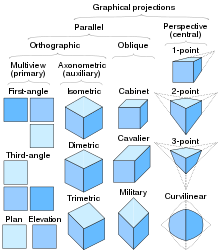
Classification of Multiview orthographic projection and some 3D projections

1. Commencement-angle projection: In this type of projection, the object is imagined to be in the first quadrant. Considering the observer normally looks from the right side of the quadrant to obtain the front view, the objects will come up in between the observer and the plane of projection. Therefore, in this instance, the object is imagined to be transparent, and the projectors are imagined to be extended from various points of the object to come across the projection plane. When these meeting points are joined in club on the aeroplane they grade an paradigm, thus in the first angle projection, any view is so placed that it represents the side of the object abroad from it. First bending projection is often used throughout parts of Europe so that it is oft called European projection.
2. 3rd-angle projection: In this type of projection, the object is imagined to exist in the tertiary quadrant. Again, every bit the observer is normally supposed to await from the right side of the quadrant to obtain the front view, in this method, the projection plane comes in between the observer and the object. Therefore, the plane of project is causeless to exist transparent. The intersection of this program with the projectors from all the points of the object would grade an prototype on the transparent plane.

Primary views [edit]

Multiview projections show the primary views of an object, each viewed in a direction parallel to i of the main coordinate axes. These primary views are called plans and elevations. Sometimes they are shown equally if the object has been cutting across or sectioned to expose the interior: these views are chosen sections.

Plan [edit]

A plan is a view of a 3-dimensional object seen from vertically to a higher place (or sometimes below^{[ commendation needed ]}). Information technology may be drawn in the position of a horizontal aeroplane passing through, above, or beneath the object. The outline of a shape in this view is sometimes called its planform, for example with shipping wings.

The program view from to a higher place a building is chosen its roof programme. A section seen in a horizontal plane through the walls and showing the floor beneath is called a floor plan.

Meridian [edit]

Height is the view of a 3-dimensional object from the position of a vertical plane beside an object. In other words, an elevation is a side view as viewed from the forepart, back, left or right (and referred to equally a front elevation, [left/ right] side elevation, and a rear top).

An elevation is a common method of depicting the external configuration and detailing of a iii-dimensional object in two dimensions. Building façades are shown every bit elevations in architectural drawings and technical drawings.

Elevations are the most common orthographic projection for conveying the appearance of a building from the exterior. Perspectives are also commonly used for this purpose. A building summit is typically labeled in relation to the compass direction it faces; the direction from which a person views it. E.g. the N Elevation of a building is the side that most closely faces true northward on the compass.^[2]

Interior elevations are used to show details such as millwork and trim configurations.

In the edifice industry elevations are non-perspective views of the structure. These are drawn to calibration so that measurements can be taken for any attribute necessary. Drawing sets include front end, rear, and both side elevations. The elevations specify the composition of the unlike facades of the building, including ridge heights, the positioning of the final fall of the land, exterior finishes, roof pitches, and other architectural details.

Adult top [edit]

A developed elevation is a variant of a regular height view in which several next non-parallel sides may exist shown together equally if they have been unfolded. For example, the north and west views may be shown side-by-side, sharing an edge, even though this does non represent a proper orthographic project.

Department [edit]

A section, or cross-section, is a view of a three-dimensional object from the position of a plane through the object.

A section is a common method of depicting the internal arrangement of a 3-dimensional object in two dimensions. It is often used in technical cartoon and is traditionally crosshatched. The fashion of crosshatching ofttimes indicates the type of cloth the section passes through.

With computed axial tomography, computers construct cross-sections from x-ray data.

• 

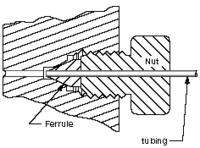
  A ii-D cross-sectional view of a compression seal.

• 

• 

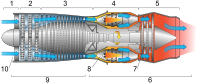
  Cross-section of a jet engine

Auxiliary views [edit]

An auxiliary view or pictorial, is an orthographic view that is projected into whatsoever plane other than one of the six primary views.^[three] These views are typically used when an object has a surface in an oblique plane. By projecting into a airplane parallel with the oblique surface, the true size and shape of the surface are shown. Auxiliary views are ofttimes drawn using isometric project.

Multiviews [edit]

Quadrants in descriptive geometry [edit]

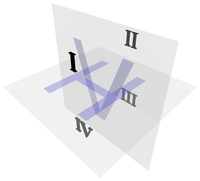
Gaspard Monge's four quadrants and 2 planes.

Modern orthographic project is derived from Gaspard Monge's descriptive geometry.^[4] Monge defined a reference system of two viewing planes, horizontal H ("ground") and vertical V ("backdrop"). These ii planes intersect to partition 3D space into 4 quadrants, which he labeled:

• I: above H, in front of V
• II: in a higher place H, behind V
• III: below H, behind V
• Iv: below H, in front of 5

These quadrant labels are the same as used in 2D planar geometry, equally seen from infinitely far to the "left", taking H and V to be the Ten-centrality and Y-axis, respectively.

The 3D object of interest is then placed into either quadrant I or III (equivalently, the position of the intersection line between the two planes is shifted), obtaining offset- and 3rd-angle projections, respectively. Quadrants II and IV are likewise mathematically valid, but their use would outcome in ane view "true" and the other view "flipped" by 180° through its vertical centerline, which is also confusing for technical drawings. (In cases where such a view is useful, east.g. a ceiling viewed from above, a reflected view is used, which is a mirror paradigm of the true orthographic view.)

Monge'southward original conception uses 2 planes merely and obtains the meridian and front views only. The addition of a third plane to testify a side view (either left or correct) is a modern extension. The terminology of quadrant is a mild anachronism, as a mod orthographic projection with three views corresponds more precisely to an octant of 3D space.

Commencement-angle project [edit]

Comparison of get-go and third-bending projections showing that related parts in the views are closer in third-angle

In get-go-angle project, the object is conceptually located in quadrant I, i.e. information technology floats above and before the viewing planes, the planes are opaque, and each view is pushed through the object onto the plane furthest from information technology. (Mnemonic: an "actor on a stage".) Extending to the 6-sided box, each view of the object is projected in the direction (sense) of sight of the object, onto the (opaque) interior walls of the box; that is, each view of the object is drawn on the opposite side of the box. A two-dimensional representation of the object is then created past "unfolding" the box, to view all of the interior walls. This produces two plans and four elevations. A simpler way to visualize this is to identify the object on pinnacle of an upside-downward bowl. Sliding the object downwards the right edge of the bowl reveals the right side view.

• 

  An paradigm of an object in a box.

• 

  The same image, with views of the object projected in the direction of sight onto walls using first-angle project.

• 

  Like image showing the box unfolding from around the object.

• 

  Paradigm showing orthographic views located relative to each other in accordance with first-bending project.

3rd-bending projection [edit]

An case of a multiview orthographic drawing from a The states Patent (1913), showing ii views of the same object. Third angle projection is used.

In tertiary-angle project, the object is conceptually located in quadrant 3, i.e. it is positioned beneath and backside the viewing planes, the planes are transparent, and each view is pulled onto the plane closest to it. (Mnemonic: a "shark in a tank", esp. that is sunken into the flooring.) Using the six-sided viewing box, each view of the object is projected reverse to the direction (sense) of sight, onto the (transparent) exterior walls of the box; that is, each view of the object is drawn on the aforementioned side of the box. The box is then unfolded to view all of its outside walls. A simpler way to visualize this is to place the object in the bottom of a bowl. Sliding the object up the right edge of the bowl reveals the right side view.

Hither is the construction of 3rd angle projections of the same object equally above. Note that the individual views are the aforementioned, simply arranged differently.

• 

• 

• 

• 

Additional data [edit]

Visualised every bit rolling on the upper and lower surfaces of the drawing aeroplane, respectively

First-angle project is as if the object were sitting on the newspaper and, from the "face" (front) view, information technology is rolled to the correct to show the left side or rolled upward to show its lesser. Information technology is standard throughout Europe and Asia (excluding Nippon). Starting time-angle projection was widely used in the Uk, just during Globe State of war II, British drawings sent to be manufactured in the USA, such equally of the Rolls-Royce Merlin, had to be drawn in tertiary-angle projection earlier they could exist produced, e.grand., as the Packard V-1650 Merlin. This meant that some British companies completely adopted tertiary angle project. BS 308 (Part 1) Applied science Drawing Exercise, gave the choice of using both projections, but generally, every illustration (other than the ones explaining the difference between beginning and 3rd-angle) was done in first-angle. After the withdrawal of BS 308 in 1999, BS 8888 offered the same selection since it referred straight to ISO 5456-2, Technical drawings – Projection methods – Part 2: Orthographic representations.

Third-angle is as if the object were a box to be unfolded. If we unfold the box then that the forepart view is in the center of the two arms, then the superlative view is in a higher place information technology, the bottom view is below it, the left view is to the left, and the right view is to the right. It is standard in the Us (ASME Y14.three-2003 specifies information technology as the default project system), Japan (JIS B 0001:2010 specifies it equally the default projection system), Canada, and Australia.

Both commencement-bending and 3rd-angle projections upshot in the aforementioned 6 views; the difference between them is the arrangement of these views around the box.

Symbol [edit]

Symbols used to define whether a projection is either showtime angle (left) or 3rd angle (right)

A bully deal of confusion has ensued in drafting rooms and applied science departments when drawings are transferred from one convention to some other. On engineering drawings, the projection is denoted by an international symbol representing a truncated cone in either first-bending or third-angle projection, as shown by the diagram on the correct.

The 3D estimation is a solid truncated cone, with the minor finish pointing toward the viewer. The front end view is, therefore, two concentric circles. The fact that the inner circle is drawn with a solid line instead of dashed identifies this view as the front view, non the rear view. The side view is an isosceles trapezoid.

• In first-bending projection, the front view is pushed dorsum to the rear wall, and the right side view is pushed to the left wall, and then the outset-angle symbol shows the trapezoid with its shortest side abroad from the circles.
• In third-angle projection, the front view is pulled forward to the front wall, and the right side view is pulled to the right wall, so the third-bending symbol shows the trapezoid with its shortest side towards the circles.

Multiviews without rotation [edit]

Orthographic multiview projection is derived from the principles of descriptive geometry and may produce an image of a specified, imaginary object equally viewed from any direction of space. Orthographic projection is distinguished past parallel projectors emanating from all points of the imaged object and which intersect of projection at right angles. Above, a technique is described that obtains varying views past projecting images after the object is rotated to the desired position.

Descriptive geometry customarily relies on obtaining diverse views past imagining an object to be stationary and changing the direction of projection (viewing) in order to obtain the desired view.

See Figure one. Using the rotation technique above, note that no orthographic view is available looking perpendicularly at any of the inclined surfaces. Suppose a technician desired such a view to, say, look through a pigsty to be drilled perpendicularly to the surface. Such a view might exist desired for computing clearances or for dimensioning purposes. To obtain this view without multiple rotations requires the principles of Descriptive Geometry. The steps below describe the employ of these principles in third angle project.

Figures one through nine.

• Fig.1: Pictorial of the imaginary object that the technician wishes to image.
• Fig.2: The object is imagined behind a vertical plane of projection. The angled corner of the plane of projection is addressed afterward.
• Fig.3: Projectors emanate parallel from all points of the object, perpendicular to the plane of projection.
• Fig.4: An image is created thereby.
• Fig.5: A second, horizontal plane of projection is added, perpendicular to the starting time.
• Fig.6: Projectors emanate parallel from all points of the object perpendicular to the second plane of project.
• Fig.7: An image is created thereby.
• Fig.8: The third plane of project is added, perpendicular to the previous two.
• Fig.9: Projectors emanate parallel from all points of the object perpendicular to the third plane of projection.

Figures ten through seventeen.

• Fig.10: An prototype is created thereby.
• Fig.11: The 4th aeroplane of projection is added parallel to the chosen inclined surface, and perforce, perpendicular to the showtime (Frontal) plane of projection.
• Fig.12: Projectors emanate parallel from all points of the object perpendicularly from the inclined surface, and perforce, perpendicular to the 4th (Auxiliary) plane of projection.
• Fig.13: An image is created thereby.
• Fig.14-16: The various planes of projection are unfolded to exist planar with the Frontal airplane of project.
• Fig.17: The terminal appearance of an orthographic multiview projection and which includes an "Auxiliary view" showing the true shape of an inclined surface.

Territorial use [edit]

Commencement-angle is used in most of the world.^[v]

Third-bending projection is most commonly used in America,^[6] Nihon (in JIS B 0001：2010);^[7] and is preferred in Australia, equally laid down in AS 1100.101—1992 6.iii.iii.^[8]

In the U.k., BS8888 9.vii.2.1 allows for three dissimilar conventions for arranging views: Labelled Views, Third Angle Projection, and Offset Angle Projection.

Come across too [edit]

• Architectural cartoon
• Cantankerous section (geometry)
• Engineering science cartoon
• Graphical projection
• Plans (drawings)

References [edit]

1. ^ Ingrid Carlbom, Joseph Paciorek (1978), "Planar Geometric Projections and Viewing Transformations", ACM Computing Surveys, ten (4): 465–502, CiteSeerXx.1.1.532.4774, doi:10.1145/356744.356750, S2CID 708008
2. ^ Ching, Frank (1985), Architectural Graphics - 2nd Edition, New York: Van Norstrand Reinhold, ISBN978-0-442-21862-one
3. ^ Bertoline, Gary R. Introduction to Graphics Communications for Engineers (quaternary Ed.). New York, NY. 2009
4. ^ "Geometric Models - Jullien Models for Descriptive Geometry". Smithsonian Institution . Retrieved 2019-12-xi .
5. ^ "Third Angle Projection". Archived from the original on March 4, 2016. Retrieved December 10, 2019.
6. ^ Madsen, David A.; Madsen, David P. (1 February 2016). Engineering science Drawing and Design. Cengage Learning. ISBN9781305659728 – via Google Books.
7. ^ "3rd Angle Projection". Musashino Fine art Academy. Retrieved 7 December 2016.
8. ^ "Full text of "Every bit 1100.101 1992 Technical Dwgs"". archive.org.

BS 308 (Role 1) Technology Drawing Practice BS 8888 Technical production documentation and specification ISO 5456-2 Technical drawings – Projection methods – Part two: Orthographic Representations (includes the truncated cone symbol)

External links [edit]

• Educational website describing the principles of beginning and third angle projection — University of Limerick
• Educational website describing the principles of starting time and third angle projection
• Images tagged "Peak" on Flickr.com
• Basic Project Method first angle vs the third angle

sotoentien.blogspot.com

Source: https://en.wikipedia.org/wiki/Multiview_orthographic_projection